Поиск кратчайшего пути
и деревья квадрантов
Как сделать быстрый поиск кратчайшего пути в реальном времени?
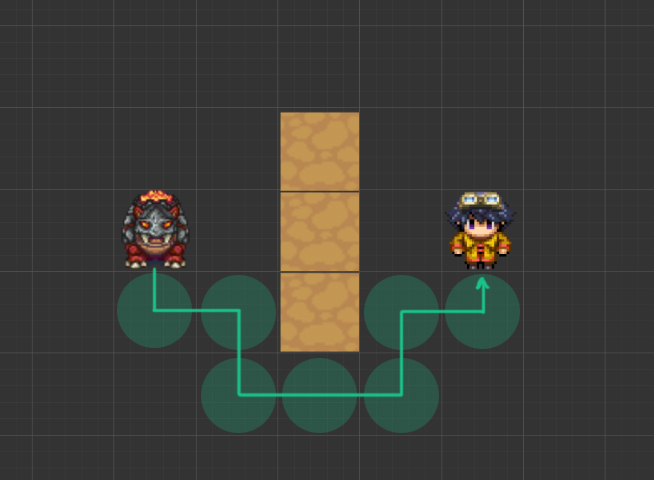
У меня в игре за игроками будут гоняться монстры, для этого нужно было реализовать какой-то алгоритм поиска пути.
Небольшой бекграунд. Проблеме нахождения кратчайшего пути десятки лет, задача звучит как поиск пути на плоскости и в общем случае нужно найти кратчайший путь из точки A в точку B, с учетом того, что есть препятствия и персонаж имеет некоторую "толстоту" :)

Это непрерывный поиск кратчайшего пути. Такая задача будет иметь очень сложное решение, это и поиск пути и какой-то raycast на тот случай, если персонаж перестанет пролазить между очередными препятствиями. Поэтому нам на помощь приходит теория графов, мы разбиваем пространство на участки квадратной формы. Каждая ячейка в такой сетке будет вершиной графа

Самое простое - это разбиение игрового мира на сетку, где расстояние перехода между соседями равно размеру клетки
Окей, мы разбили мир на сетку, теперь путь можно проложить по клеткам. Диагональных переходов нет, потому что в общем случае нельзя гарантировать, что персонаж не зацепится за стенку и не застрянет. Теперь у нас есть граф, где каждая клетка это вершина.
Как искать путь?
Как искать путь?
Был алгоритм Дейкстры, который в последствии был улучшен и назван A*
Объяснить лучше чем на википедии вряд ли получится. Но смысл очень простой
Каждая клетка характеризуется кратчайшим путем к ней из начальной. И родительской клеткой, из которой мы в нее попали
Начинаем двигаться от начальной точки, открываем соседние вершины по принципу наименьшего расстояния.
На подсчете расстояния стоит остановиться по-подробнее. Давайте в качестве эвристического расстояния из клетки А к его соседу B считать как расстояние перехода из A в B (который равен размеру клетки) + расстояние от B до конечной точки. Мы добавляем расстояние до конечной точки затем, чтобы при выборе лучшей открытой точки, мы выбирали ту, которая потенциально ближе. Именно поэтому на гифке справа сначала открываются диагональные ячейки по направлению к конечной точки.
Это эвристическое расстояние, то есть мы предполагаем что оно отражает расстояние до конечной клетки. Но в реальности оно может часто заводить в тупики, см. гифку
Таким образом когда мы будем сортировать открытые клетки, первой будет браться та, которая кажется ближе к конечной точке.
Каждая итерация будет заключаться в
1) выбор открытой клетки с наименьшим расстоянием, для того чтобы продолжить лучший на данный момент путь
2) добавление ее соседей в список открытых клеток
3) если мы к уже закрытой клетке пришли более коротким путем, то ее родительская клетка меняется на текущую а путь перезаписывается
4) клетка помечается закрытой и удаляется из списка
5) когда мы достигаем конечной клетки, или мы обошли все клетки и не нашли пути - алгоритм прекращает работу.
Объяснить лучше чем на википедии вряд ли получится. Но смысл очень простой
Каждая клетка характеризуется кратчайшим путем к ней из начальной. И родительской клеткой, из которой мы в нее попали
Начинаем двигаться от начальной точки, открываем соседние вершины по принципу наименьшего расстояния.
На подсчете расстояния стоит остановиться по-подробнее. Давайте в качестве эвристического расстояния из клетки А к его соседу B считать как расстояние перехода из A в B (который равен размеру клетки) + расстояние от B до конечной точки. Мы добавляем расстояние до конечной точки затем, чтобы при выборе лучшей открытой точки, мы выбирали ту, которая потенциально ближе. Именно поэтому на гифке справа сначала открываются диагональные ячейки по направлению к конечной точки.
Это эвристическое расстояние, то есть мы предполагаем что оно отражает расстояние до конечной клетки. Но в реальности оно может часто заводить в тупики, см. гифку
Таким образом когда мы будем сортировать открытые клетки, первой будет браться та, которая кажется ближе к конечной точке.
Каждая итерация будет заключаться в
1) выбор открытой клетки с наименьшим расстоянием, для того чтобы продолжить лучший на данный момент путь
2) добавление ее соседей в список открытых клеток
3) если мы к уже закрытой клетке пришли более коротким путем, то ее родительская клетка меняется на текущую а путь перезаписывается
4) клетка помечается закрытой и удаляется из списка
5) когда мы достигаем конечной клетки, или мы обошли все клетки и не нашли пути - алгоритм прекращает работу.

Работа алгоритма A*
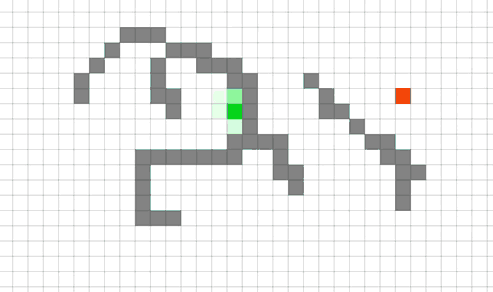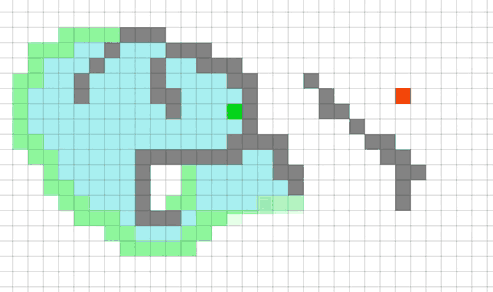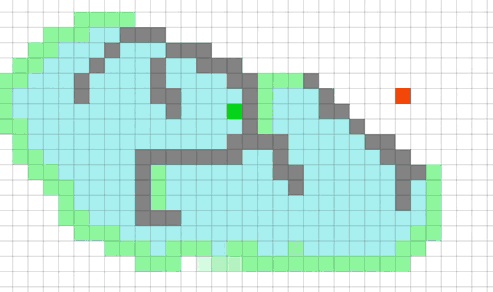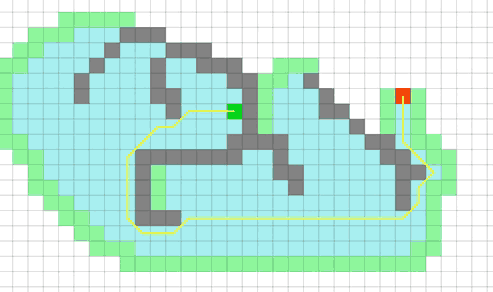
Можно обратить внимание, как алгоритм "переключается" на дальние варианты, когда сортировка открытых клеток (зеленые) подсовывает ему очень далекую клетку в качестве лучшей
Теперь мы можем разбить карту на сетку, определить является ли стенка клеткой,
найти для каждой клетки соседей. Что дальше?
найти для каждой клетки соседей. Что дальше?
Новые посты публикую в твиттере https://twitter.com/DorogoyYuriy
Проблема такого подхода заключается в том, что клеток очень много, и, если брать к примеру игры, то искать абсолютно кратчайший путь не нужно. А нужно искать путь быстро. Очевидно, что пространства можно группировать определенным образом. И игровые пространства обычно характерны определенной "комнатностью", а значит клетки можно сгрупировать как одну
Для своих задач я выбрал один из самых простых вариантов разбиения - это деревья квадрантов (Quadtrees). Есть и другие варианты, кстати по ссылке отличия разных способов разбиения
Идея очень простая - разбиваем пространство на большие блоки, к примеру 500px * 500px. Если блок пересекается со стенкой, мы начинаем дробить его на 4 подблока - квадранта. Если подблок не пересекается со стенкой, мы оставляем его в покое. В противном случае запускаем рекурсивно эту же операцию для всех квадрантов.
Помимо уменьшения количества клеток, для среднего случая когда игрок и монстр находятся посредине комнаты, мы получим намного меньше проверок
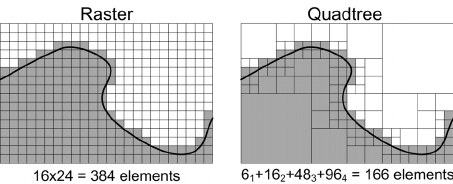
Смысл более-менее понятне, перейдем к коду. Давайте опишем структуру PFBox - это обычный AABB, параллелепипед
он умеет проверять пересечения с такими же PFBox методом intersects. И определять содержит ли в себе другой бокс с помощью contains. Константа cellSize - размер минимального квадранта в пикселях.
он умеет проверять пересечения с такими же PFBox методом intersects. И определять содержит ли в себе другой бокс с помощью contains. Константа cellSize - размер минимального квадранта в пикселях.
package main
import (
"container/heap"
"math"
)
const cellSize = 25.
type PFBox struct {
x1 float64
x2 float64
y1 float64
y2 float64
}
func (b *PFBox) width() float64 {
return b.x2 - b.x1
}
func (b *PFBox) height() float64 {
return b.y2 - b.y1
}
func (b *PFBox) contains(x float64, y float64) bool {
return (b.x1 < x && x < b.x2 && b.y1 < y && y < b.y2)
}
func (b *PFBox) intersects(box *PFBox) bool {
return (b.x1 <= box.x2 && box.x1 <= b.x2 && b.y1 <= box.y2 && box.y1 <= b.y2)
}
func CreateSquarePFBox(cx float64, cy float64, side float64) *PFBox {
halfSide := side / 2
return &PFBox{x1: cx - halfSide, y1: cy - halfSide, x2: cx + halfSide, y2: cy + halfSide}
}
Теперь давайте опишем структуру PFNodeTree. Это структура ячейки, которая умеет дробиться на такие же.
x, y, region - координаты и размеры клетки.
level - глубина, чем выше уровень тем выше клетка в иерархии
root - корневая клетка
crossable определяет, можно ли через эту клетку идти и фактически означает стенка это или нет.
если isLeaf равное true, то это лист и он не содержит дочерних квадрантов
quads - сами квадранты
neighbors - соседи клетки, хочу обратить внимание, что соседом может быть клетка большего размера
heuristic - эвристическое расстояние, упомянутое выше
heapInx - индекс открытой клетки в массиве (куче, если быть точным)
listId - уникальный Id текущей итерации поиска. Определяет содержится ли клетка в списке открытых вершин, пройденных (закрытых) или эту вершину еще не обрабатывали
x, y, region - координаты и размеры клетки.
level - глубина, чем выше уровень тем выше клетка в иерархии
root - корневая клетка
crossable определяет, можно ли через эту клетку идти и фактически означает стенка это или нет.
если isLeaf равное true, то это лист и он не содержит дочерних квадрантов
quads - сами квадранты
neighbors - соседи клетки, хочу обратить внимание, что соседом может быть клетка большего размера
heuristic - эвристическое расстояние, упомянутое выше
heapInx - индекс открытой клетки в массиве (куче, если быть точным)
listId - уникальный Id текущей итерации поиска. Определяет содержится ли клетка в списке открытых вершин, пройденных (закрытых) или эту вершину еще не обрабатывали
type PFNodeTree struct {
x float64
y float64
level int
listId int
heuristic float64
region *PFBox
root *PFNodeTree
crossable bool
isLeaf bool
quads []*PFNodeTree
neighbors []*PFNodeTree
heapInx int
pathParent *PFNodeTree
}CreatePFNodeTree создает объект клетки с заданными параметрами
getQuad - получает квадрант по координатам
get - рекурсивно ищет квадрант нижнего уровня
getQuad - получает квадрант по координатам
get - рекурсивно ищет квадрант нижнего уровня
func CreatePFNodeTree(region *PFBox, obstacles []*PFBox, root *PFNodeTree, level int) *PFNodeTree {
n := PFNodeTree{}
n.quads = make([]*PFNodeTree, 4)
n.level = level
if root != nil {
n.root = root
} else {
n.root = &n
}
n.region = region
n.x = (region.x1 + region.x2) / 2
n.y = (region.y1 + region.y2) / 2
n.obstacles = obstacles
n.crossable = true
n.isLeaf = false
if len(n.obstacles) == 0 {
n.isLeaf = true
} else if n.level == 0 {
n.isLeaf = true
n.crossable = false
}
return &n
}
func (n *PFNodeTree) getQuad(x float64, y float64) *PFNodeTree {
if x < n.x && y < n.y {
return n.quads[0]
} else {
if x >= n.x && y < n.y {
return n.quads[1]
} else if x < n.x && y >= n.y {
return n.quads[2]
}
}
return n.quads[3]
}
func (n *PFNodeTree) get(x float64, y float64) *PFNodeTree {
if !n.region.contains(x, y) {
return nil
}
if n.isLeaf {
return n
}
return n.getQuad(x, y).get(x, y)
}update - рекурсивно разбивает клетки на квадранты. Если квадрант пересекается с препятствиями, то subregionObstacles не пустой. В противном случае при вызове CreatePFNodeTree мы поставим crossable = false
func (n *PFNodeTree) update() {
if n.isLeaf {
return
}
l := n.region.x1
r := n.region.x2
t := n.region.y1
b := n.region.y2
x := n.x
y := n.y
subregions := []*PFBox{
&PFBox{x1: l, y1: t, x2: x, y2: y},
&PFBox{x1: x, y1: t, x2: r, y2: y},
&PFBox{x1: l, y1: y, x2: x, y2: b},
&PFBox{x1: x, y1: y, x2: r, y2: b},
}
for i, subregion := range subregions {
var subregionObstacles []*PFBox
for _, obstacle := range n.obstacles {
if subregion.intersects(obstacle) {
subregionObstacles = append(subregionObstacles, obstacle)
}
}
n.quads[i] = CreatePFNodeTree(subregion, subregionObstacles, n.root, n.level-1)
n.quads[i].update()
}
}getNeighbors - функция, которая умеет искать соседей. Ничего криминального, ищем вокруг текущей клетки соседей с шагом cellSize. Если такого соседа еще не было - добавляем. И сохраняем результат в n.neighbors
func (n *PFNodeTree) getNeighbors() []*PFNodeTree {
if n.neighbors != nil {
return n.neighbors
}
left := n.region.x1
right := n.region.x2
top := n.region.y1
bottom := n.region.y2
minCell := cellSize
possibleNeighbors := math.Pow(2, float64(n.level))
var neighbors PFNodeHeap
for x := -(possibleNeighbors + 1); x <= (possibleNeighbors + 1); x += 2 {
xx := n.x + minCell*(x/2)
neighbor := n.root.get(xx, top-minCell/2)
if neighbor != nil && neighbor.crossable && !neighbors.has(neighbor) {
neighbors = append(neighbors, neighbor)
}
neighbor = n.root.get(xx, bottom+minCell/2)
if neighbor != nil && neighbor.crossable && !neighbors.has(neighbor) {
neighbors = append(neighbors, neighbor)
}
}
for y := -(possibleNeighbors - 1); y <= (possibleNeighbors - 1); y += 2 {
yy := n.y + minCell*(y/2)
neighbor := n.root.get(left-minCell/2, yy)
if neighbor != nil && neighbor.crossable && !neighbors.has(neighbor) {
neighbors = append(neighbors, neighbor)
}
neighbor = n.root.get(right+minCell/2, yy)
if neighbor != nil && neighbor.crossable && !neighbors.has(neighbor) {
neighbors = append(neighbors, neighbor)
}
}
n.neighbors = neighbors
return n.neighbors
}Давайте опишем класс PFNodeHeap, который будет реализовывать интерфейс из библиотеки container/heap. Куча, как структура данных это двоичное дерево, чтобы мы быстро могли получить минимум или максимум. Почитайте здесь. Метод Pop() достает максимальный или минимальный элемент, в зависимости от вашей сортировки, за время O(1), а вставка происходит за O(log n) операций.
Для работы с container/heap наша структура должна реализовать 3 метода, Len - получение длины. Less - выбор наименьшего из двух, сравнение эвристических расстояний в нашем случае. Swap - перестановка указателей, heapInx - индекс объекта в куче, нужно переставить отдельно. Push и Pop - добавление и получение "лучшего".
Для работы с container/heap наша структура должна реализовать 3 метода, Len - получение длины. Less - выбор наименьшего из двух, сравнение эвристических расстояний в нашем случае. Swap - перестановка указателей, heapInx - индекс объекта в куче, нужно переставить отдельно. Push и Pop - добавление и получение "лучшего".
type PFNodeHeap []*PFNodeTree
func (nn PFNodeHeap) has(n *PFNodeTree) bool {
for _, c := range nn {
if c == n {
return true
}
}
return false
}
func (h PFNodeHeap) Len() int { return len(h) }
func (h PFNodeHeap) Less(i, j int) bool { return h[i].heuristic < h[j].heuristic }
func (h PFNodeHeap) Swap(i, j int) {
h[i].heapInx, h[j].heapInx = h[j].heapInx, h[i].heapInx
h[i], h[j] = h[j], h[i] }
func (h *PFNodeHeap) Push(x interface{}) {
item := x.(*PFNodeTree)
item.heapInx = len(*h)
*h = append(*h, x.(*PFNodeTree))
}
func (h *PFNodeHeap) Pop() interface{} {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}Можно перейти к самому алгоритму кратчайшего пути. В данном случае это будет A*. Опишем глобальную функцию distance. Отсутствие квадратного корня здесь не случайно, это одна из оптимизаций, которая делает поиск не очень точным, но мы не считаем квадратный корень.
unqiueListID используется, чтобы отделить предыдущие итерации от текущей. То есть если n.listId = closedId, то эта клетка была закрыта за текущую итерацию. Если n.listId = openId - еще открыта. Это избавляет от перезаписывания всех listId по всему дереву.
unqiueListID используется, чтобы отделить предыдущие итерации от текущей. То есть если n.listId = closedId, то эта клетка была закрыта за текущую итерацию. Если n.listId = openId - еще открыта. Это избавляет от перезаписывания всех listId по всему дереву.
func distance(a *PFNodeTree, b *PFNodeTree) float64 {
x_dist := b.x - a.x
y_dist := b.y - a.y
return x_dist*x_dist + y_dist*y_dist
}
func (n *PFNodeTree) PathFind(p1 *Vec2, p2 *Vec2) []*Vec2 {
unqiueListID += 2
closedId := unqiueListID - 1
openId := unqiueListID
src := n.get(p1[0], p1[1])
dst := n.get(p2[0], p2[1])
if !dst.crossable {
dst = dst.getCrossableNeighbor()
}
//Для того, чтобы монстр не ходил всегда в притирку со стенкой, я сделал препятствия
//шире на ~20px, поэтому иногда игрок может стоять в "стенке"
//Поэтому если конечная точка находится в стенке, мы идем к ближайшему соседу
var traveled = make(map[*PFNodeTree]float64)
//Посещенные за эту итерацию клетки вместе с их расстояниями
src.listId = openId
if src == dst {
return []*Vec2{p2}
} else {
traveled[src] = 0
src.pathParent = src
dst.pathParent = nil
src.heuristic = distance(src, dst)
open := &PFNodeHeap{}
heap.Init(open)
heap.Push(open, src)
//Инициализируем кучу, добавляем первую клетку
for len(*open) > 0 {
current := heap.Pop(open).(*PFNodeTree)
//В цикле берем лучшую на данный момент клетку и пытаемся улучшить ее путь
if current == dst {
break //конечная клетка достигнута
}
current.listId = closedId
var neighbors = current.getNeighbors()
//получаем список соседей
for _, neighbor := range neighbors {
if neighbor.listId == closedId {
continue //пропускаем соседей обработанных за эту операцию
}
var oldPath float64 = math.Inf(1)
tr, _ := traveled[neighbor]
if tr > 0 {
oldPath = tr
}
//Предыдущий путь равен либо значению traveled для этой клетки, а если его нет
// то присваиваем бесконечности
var replacedPath float64 = -1
newPath := traveled[current] + distance(current, neighbor)
//Пересчитываем новый путь попадания в соседа,
//равный путь к текущей клетке + расстояние к соседу
if newPath < oldPath {
//Если путь короче, то перезаписываем родительскую клетку
//эвристическое расстояние
traveled[neighbor] = newPath
neighbor.pathParent = current
neighbor.heuristic = newPath + distance(neighbor, dst)
// Если сосед есть в списке, то обновляем его место в массиве методом Fix
// Иначе, добавляем новый элемент
if neighbor.listId == openId {
heap.Fix(open, neighbor.heapInx)
} else {
heap.Push(open, neighbor)
neighbor.listId = openId
}
}
}
}
}
}
if dst.pathParent == nil {
return []*Vec2{p2} //Путь заблокирован
}
var pathNodes []*PFNodeTree = make([]*PFNodeTree, 0)
var node = dst
for node != src {
pathNodes = append([]*PFNodeTree{node}, pathNodes...)
node = node.pathParent
if node == nil {
break
}
}
//Сглаживаем путь, об этом ниже
return n.lerpPath(pathNodes)
}
Вот так выглядит наш монстр, который теперь может динамически находить путь к игроку
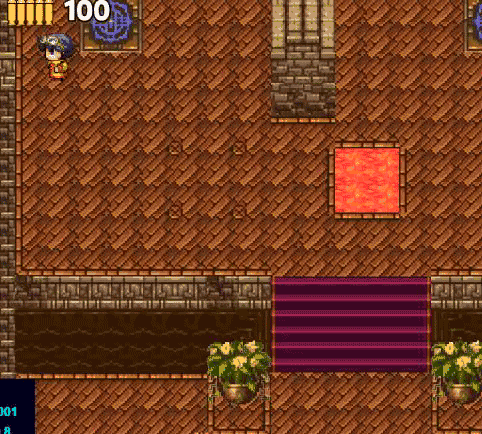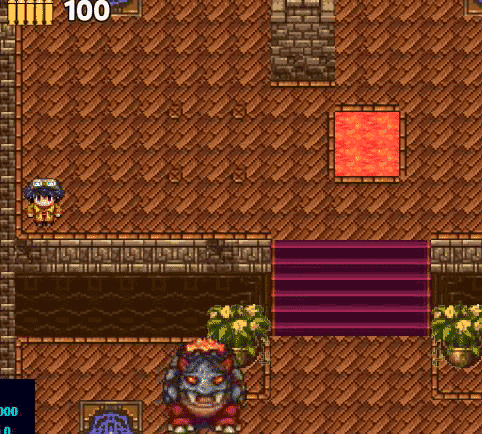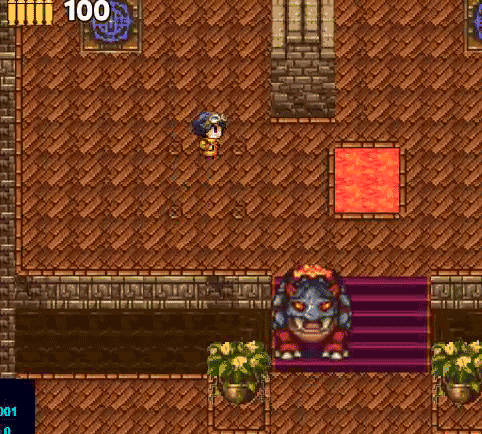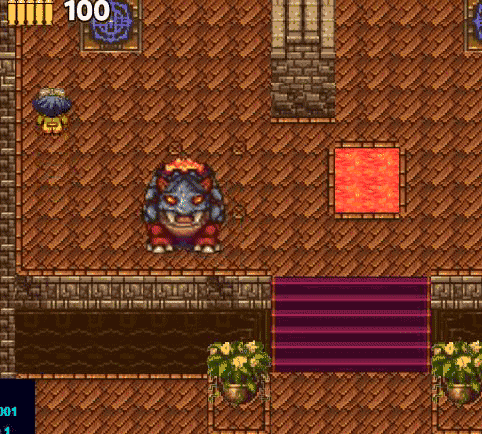
А вот наш quad tree. Можно заметить, что стенок чуть больше, чем есть на самом деле. Это для того, чтобы путь монстра выглядел естественнее.
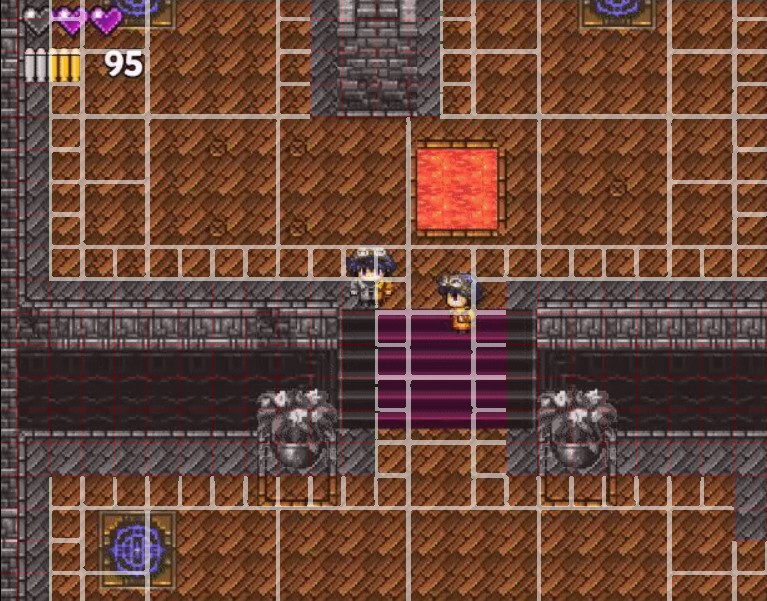
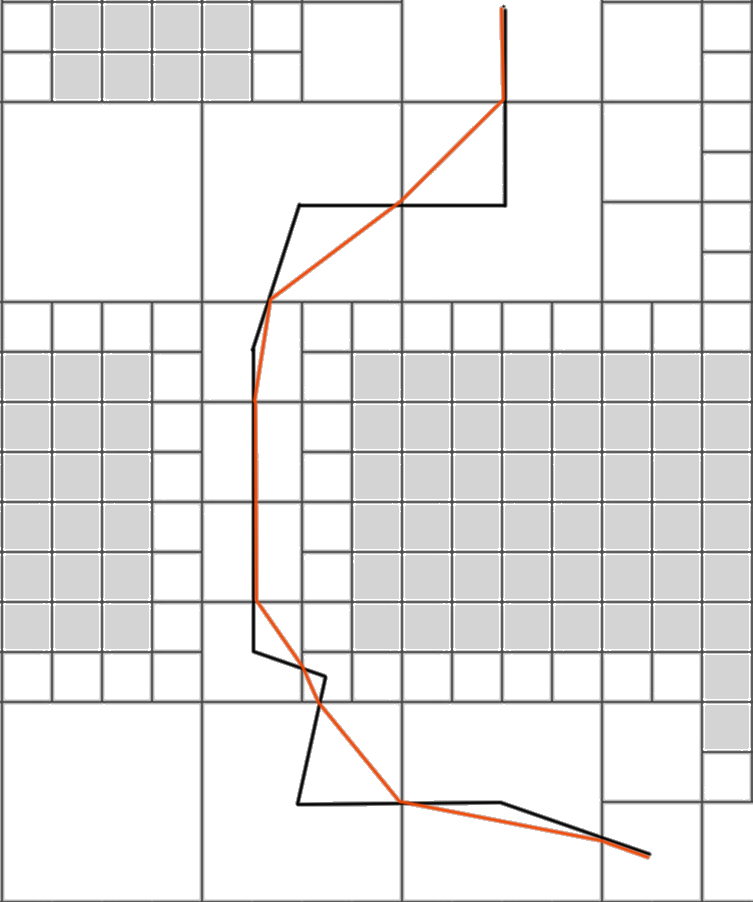
Можно заметить, что оранжевый путь получается и короче и естественнее
Последняя часть, на которой хочется остановиться - это перемещение между клетками высокого уровня, т.е. большими клетками.
Так как путь состоит из клеток, если быть точным их центров, то он получается очень угловатым, выделено черным на картинке. Самое простое сглаживание, которое приходит на ум - это находить пересечения с границами клеток и соединять уже их в качестве пути - выделено оранжевым.
Так как путь состоит из клеток, если быть точным их центров, то он получается очень угловатым, выделено черным на картинке. Самое простое сглаживание, которое приходит на ум - это находить пересечения с границами клеток и соединять уже их в качестве пути - выделено оранжевым.
Скачать модуль целиком можно здесь
По вопросам обращайтесь ddearcj@gmail.com
